一、由最朴素的负二项分布引入
笔者近来养成了写作业时喜欢听歌的坏习惯,某日学习《概率论》的时候在歌单里找到了A歌曲,从此首歌开始随机播放歌单里的所有歌曲(为取一般性,歌单一共![]() 首歌,平均取每首歌时长
首歌,平均取每首歌时长![]() 分钟),并决定下一次听到A歌曲的时候就停止学习。为了让学习时长看上去不那么模糊,笔者选择计算一下学习时长的期望。
分钟),并决定下一次听到A歌曲的时候就停止学习。为了让学习时长看上去不那么模糊,笔者选择计算一下学习时长的期望。
问题可以简化为:定下第一首歌为A,后续的每一首歌都等可能地从![]() 首歌里选择,记
首歌里选择,记![]() 为下一次听到A歌前听的歌曲数目(包括定下的第一首A歌曲),即求
为下一次听到A歌前听的歌曲数目(包括定下的第一首A歌曲),即求![]() 。
。
这是一个最朴素的负二项分布,我们有
![]()
很容易算出期望
![Rendered by QuickLaTeX.com \[E[X]=\sum_{k=1}^{+\infty}kP(X=k)\]](https://timetown.site/wp-content/ql-cache/quicklatex.com-67983fea9a364359854ccb3be453d6d0_l3.png)
代入有
![Rendered by QuickLaTeX.com \[E[X]=\sum_{k=1}^{+\infty}k\left(\frac{N-1}{N}\right)^{k-1}\frac{1}{N}\]](https://timetown.site/wp-content/ql-cache/quicklatex.com-cb6469bb5ff10dd68ef7ccc514573bb8_l3.png)
运用一下高中的错位相减法并取一下极限即可得到
![Rendered by QuickLaTeX.com \[E[X]=\sum_{k=1}^{+\infty}\left(\frac{N-1}{N}\right)^{k-1}=N\]](https://timetown.site/wp-content/ql-cache/quicklatex.com-b0bb0afb1a09f10e3a93e271c1f5b876_l3.png)
这样,笔者平均学习![]() 时长就可以停止学习了。
时长就可以停止学习了。
这个随机播放的模型看上去很正常,期望是歌单内的总歌曲数目也符合实际,但是细究一下会发现,看上去的“随机播放”在用户体感上可能并不随机。
二、出现问题
如果我们考虑![]() ,即播放不到
,即播放不到![]() 首歌就能再次听到A歌曲的概率,就可以发现
首歌就能再次听到A歌曲的概率,就可以发现
![Rendered by QuickLaTeX.com \[P(X\le k)=\sum_{i=1}^{k}P(X=i)\]](https://timetown.site/wp-content/ql-cache/quicklatex.com-cc39c4470dfc17cac0ae30ffea87a46e_l3.png)
代入有
![]()
我们取
![Rendered by QuickLaTeX.com \[P(X\le k)=1-\left(1-\frac{1}{N}\right)^{\tilde{k}N}\]](https://timetown.site/wp-content/ql-cache/quicklatex.com-b43034a6d083d243c872469d122f3b28_l3.png)
如果歌单中歌曲总数![]() 不算太小的时候(以笔者歌单中的40首歌为例,
不算太小的时候(以笔者歌单中的40首歌为例,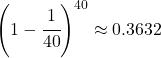 ,而
,而![]() ,也就是说在歌单歌曲数在40左右时,就已经有很好的近似程度了),上式趋近于
,也就是说在歌单歌曲数在40左右时,就已经有很好的近似程度了),上式趋近于
![]()
这样看可能不太直观,我们不妨取一个具体的![]() ,得到约有
,得到约有![]() 的概率在听完不到五分之一的歌曲之后就会听到A歌曲。也就是说笔者有
的概率在听完不到五分之一的歌曲之后就会听到A歌曲。也就是说笔者有![]() 的概率在听完不到五分之一的歌曲之后就可以停止学习。由于学习次数的基数大,那么遇到这种情况的次数不会很低,再加上人通常对小概率事件的注意力更多,因此体感上笔者会觉得学了一学期之后,经常能碰到单次学习时长只有期望的五分之一的情况。
的概率在听完不到五分之一的歌曲之后就可以停止学习。由于学习次数的基数大,那么遇到这种情况的次数不会很低,再加上人通常对小概率事件的注意力更多,因此体感上笔者会觉得学了一学期之后,经常能碰到单次学习时长只有期望的五分之一的情况。
往大处看,由于音乐软件用户基数大,最后![]() 的人数量会很多,而在这些用户的体感上来看,“随机播放”看上去也没有那么随机了。此时,真随机在体感上来看不像是随机。
的人数量会很多,而在这些用户的体感上来看,“随机播放”看上去也没有那么随机了。此时,真随机在体感上来看不像是随机。
三、试图缓解问题
既然最朴素的真随机在体感上不像是随机,那么我们就试图开拓一个新的随机播放形式,使得随机播放不再是真随机,但是在体感上看来更像是随机播放。
接下来所用符号,如无特别说明,与前文一致。
我们现在可以虚构出一个程序,它能使得任意两首相同的歌曲之间至少有![]() 首歌,即在下一次听到A歌曲之前,至少已经听了
首歌,即在下一次听到A歌曲之前,至少已经听了![]() 首歌。这样的话,我们至少可以保证:
首歌。这样的话,我们至少可以保证:
不会再发生原先约![]() 的人在听完不到
的人在听完不到![]() 比例的歌就能再听到A歌曲的情况,从而在体感上让他们感觉“随机播放”确实是“随机”的。
比例的歌就能再听到A歌曲的情况,从而在体感上让他们感觉“随机播放”确实是“随机”的。
此时我们不妨也算一算,在虚构程序的干预下,下一次再听到A歌曲前听的歌曲数目的期望。
这里我们可以做一个简单的模型来便于理解这个虚构程序。假设有一个池子里放了![]() 个小球,每次从里面拿一个小球拿在手上(注意要保留顺序),然后直到手上的小球数达到
个小球,每次从里面拿一个小球拿在手上(注意要保留顺序),然后直到手上的小球数达到![]() 个时,下一次拿球的时候就要弃置手上的最早拿的球。如此往复。现在我们的问题是一开始取到的小球标记为A,然后按上述规则不断拿球,直到再次拿到A球,此时统计一下之前拿的球数记为
个时,下一次拿球的时候就要弃置手上的最早拿的球。如此往复。现在我们的问题是一开始取到的小球标记为A,然后按上述规则不断拿球,直到再次拿到A球,此时统计一下之前拿的球数记为![]() 。稍加思考便知此模型与随机播放歌曲的模型等价。接下来开始正式求期望。
。稍加思考便知此模型与随机播放歌曲的模型等价。接下来开始正式求期望。
首先,由于虚构程序的干预,我们有
![]()
![]()
第二个式子前省略了
依照此思想可以得到后续的概率![]() 为
为![]()
![]()
万事俱备,我们可以求期望了。得到
![Rendered by QuickLaTeX.com \[E[X]=\sum_{i=1}^{+\infty}iP(X=i)\]](https://timetown.site/wp-content/ql-cache/quicklatex.com-aa167b400060fa83d6ee6da816f1c42e_l3.png)
同理运用一下错位相减即得
![Rendered by QuickLaTeX.com \[E[X]=k+\sum_{i=1}^{+\infty}\left(\frac{N-k-1}{N-k}\right)^{i-1}\]](https://timetown.site/wp-content/ql-cache/quicklatex.com-a89fdfe8a042e35f9d8fa2eebc8fa1c3_l3.png)
化简得到
![]()
于是我们得到了一个惊人的结论,即在虚构程序的作用下,下一次听到A歌前听到的歌曲数的期望总是![]() 。也就是说,我们虚构出的程序在不改变总期望的情况下,减少了用户体感上的“不随机感”,因此这个虚构程序看起来较为成功。
。也就是说,我们虚构出的程序在不改变总期望的情况下,减少了用户体感上的“不随机感”,因此这个虚构程序看起来较为成功。
四、模型的延伸思考
最后,我们可以改变此模型中的![]() 来达到不同程度上的“体感随机性”。
来达到不同程度上的“体感随机性”。
1.若取![]() ,那么此模型就变回了最开始的朴素的真随机播放模式。
,那么此模型就变回了最开始的朴素的真随机播放模式。
2.若取![]() ,则在听到下一次A歌曲之前,歌单内的所有歌曲都会被播放且仅播放一次,且之后的播放会严格按照第一轮播放歌曲的顺序播放,算得上是一种“用户无法操控”的顺序播放(这里用户无法操控的意思是,用户从第二轮播放开始,就能察觉到歌曲播放顺序被固定,但是无法做到播放之前就确定下来歌曲播放的顺序)。
,则在听到下一次A歌曲之前,歌单内的所有歌曲都会被播放且仅播放一次,且之后的播放会严格按照第一轮播放歌曲的顺序播放,算得上是一种“用户无法操控”的顺序播放(这里用户无法操控的意思是,用户从第二轮播放开始,就能察觉到歌曲播放顺序被固定,但是无法做到播放之前就确定下来歌曲播放的顺序)。
至此,我们由一个平常的随机播放问题,引出了一个数学问题,并建立了一个虚构程序来解决问题。
顺利产出一篇学术垃圾(bushi)


不是学术垃圾啊,这对我很有帮助(●’◡’●)
感谢你的支持:-)
鸡排饭好吃( ̄︶ ̄)